EXPERIMENTO B: Combinaciones
Para entender una ciudad debemos ocuparnos de lo esencial, del fenómeno primario: las combinaciones o mezcla de usos, no la separación y aislamiento de ellos. Ya vimos esto en el caso de los parques vecinales. La diversidad urbana origina, permite y estimula más diversidad.
JANE JACOBS,
Muerte y vida de las grandes ciudades, (Capitan Swing, 2011) originalmente publicada como The Death and Life of Great American Cities (1961)
Pareciera que los textos de Jacobs nos marcan el guion perfecto para afrontar la línea argumental de estas experiencias. Más allá de la aproximación inicial en la que solo expusimos el trabajo con cultivos, traemos aquí el aprendizaje que sentará la complejidad para el estudio dinámico final.
Las mezclas complejas de usos diferentes no son en modo alguno una forma particular de caos, al menos no desde una interpretación peyorativa de este. Representan una forma de orden compleja y altamente desarrollada.
¿Cuál es el propósito del modelo?
Estudiar el reparto distribuido de habitantes en un entorno urbano genérico, a través de una serie de patrones geométricos y de usos, en una situación estática.
¿Cómo utilizaremos la herramienta y su interfaz?
Como presentamos en el caso anterior exploraremos el espacio tridimensional de la herramienta, pero en este caso desde tres maneras potenciales: la gestión de mallas, que nos servirán como entrada para el terreno, la extrusión ampliada, de distintos datos, de la edificación y la visualización de enlaces entre capas de usos.
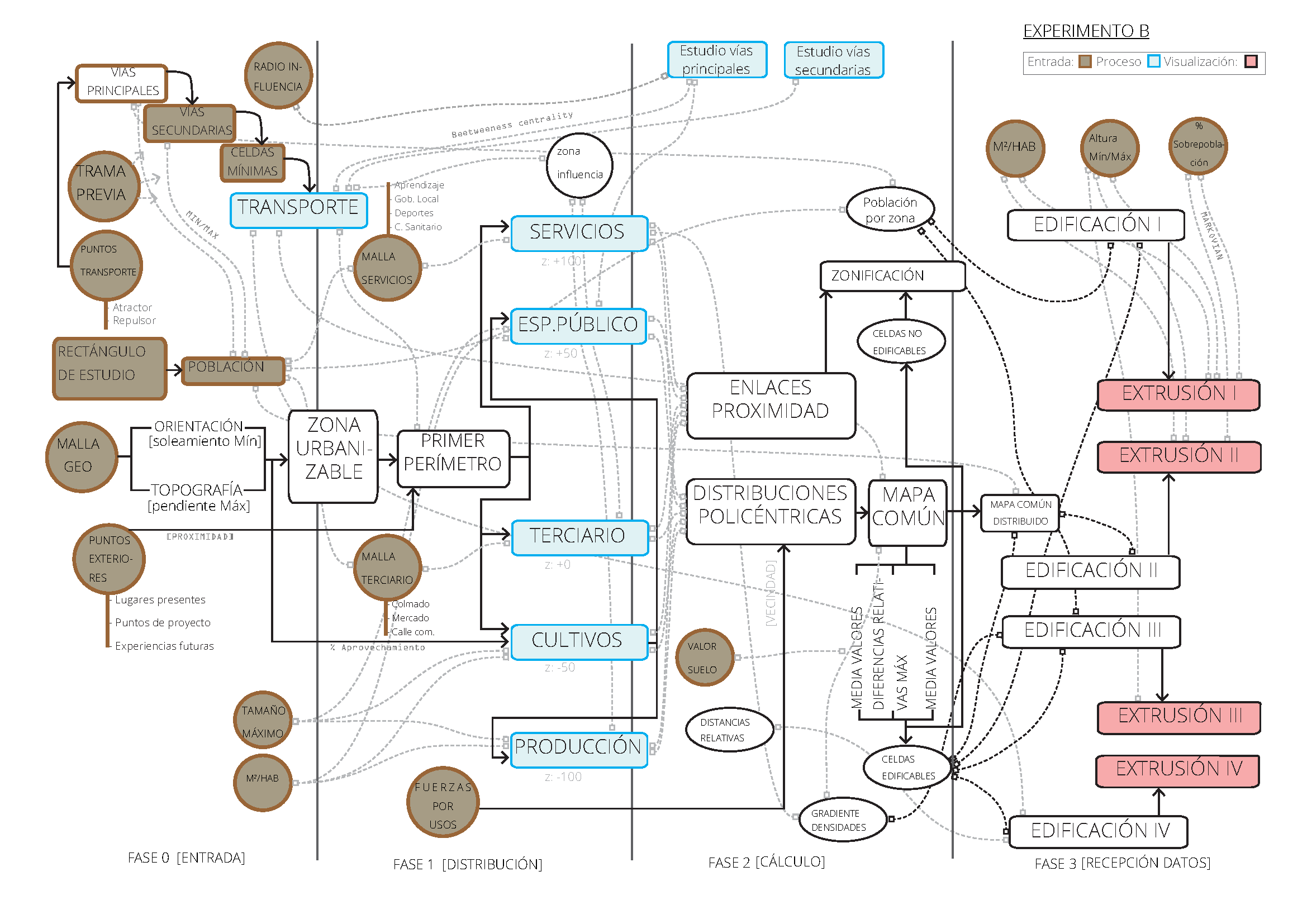
El experimento se dividirá en 4 fases diferenciadas.
– Fase 0 [Entrada]
– Fase 1 [Distribución]
– Fase 2 [Cálculo]
– Fase 3 [Recepción Datos]
La distribución de capas que se aprecia a la derecha refleja el campo de trabajo sobre la coordenada “z” en la herramienta. Esto resulta más transcendental que el simple orden visual directo, pues también expone por su distancia al plano (0,0), el orden de influencia de los usos entre sí, incluyendo el orden de entrada de la zonificación.
El diagrama de la siguiente página muestra el desglose por fases y la capacidad de control sobre los cálculos en la línea argumental del experimento.
FASE 0. ENTRADA
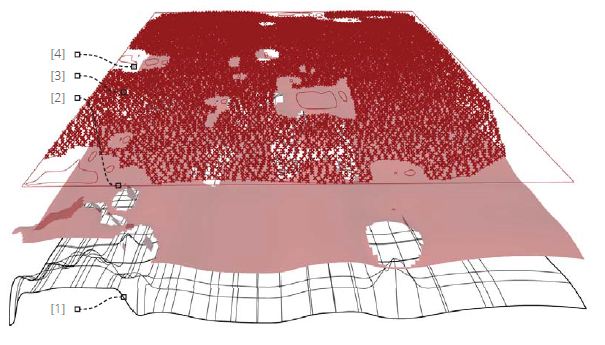 El primer apoyo para un contexto de trabajo, como ocurria en el caso anterior, será la posibilidad de gestionar la topografía como malla, lo que nos permite conocer las pendientes y el ángulo de soleamiento de cada cara, filtrando estos sectores hacia una zona “urbanizable”, por los propios condicionantes.
El primer apoyo para un contexto de trabajo, como ocurria en el caso anterior, será la posibilidad de gestionar la topografía como malla, lo que nos permite conocer las pendientes y el ángulo de soleamiento de cada cara, filtrando estos sectores hacia una zona “urbanizable”, por los propios condicionantes.
En este momento procedemos a la distribución del conjunto de habitantes con los que vamos a plantear el proyecto, como puntos con un grado de aleatoriedad, en la superficie filtrada. Aunque trabajemos posteriormente para definir el “primer perímetro”, la herramienta nos exigirá un rectángulo límite para el reparto de los punto. Este surge de la aplicación de la densidad global.
Para afrontar la cuestión de la movilidad de una manera que integre el contexto inicial de estudio, incorporamos el recurso de unos puntos exteriores que interactuaran con el sistema de transporte, convirtiéndose en enlaces al conjunto de vías principales.
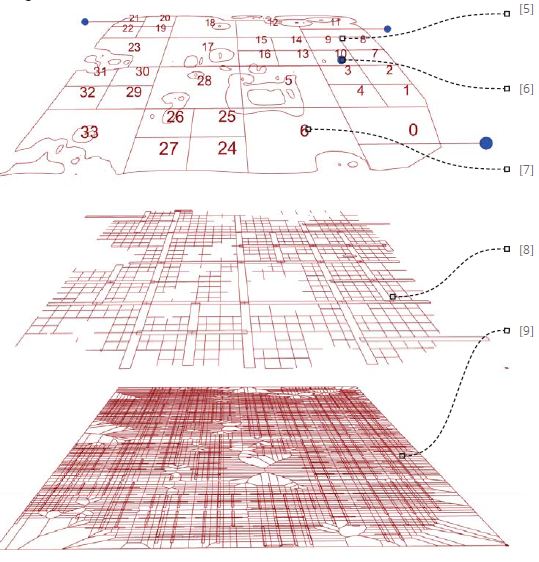 En la presentación de GH calculábamos las áreas de transporte local y vecindades por su relación geométrica, a través de cuadrículas delimitadas por las distancias entre vías. En este caso y para un trabajo más interesante hacia el estudio de la densidad, las compondremos a partir de un número máximo de habitantes por zona, utilizando la división matemática del árbol cuaternario que nos permite condicionar rectángulos a partir del número de puntos en su interior. Esta operación le añade el protagonismo que merecía al estudio sobre la población y nos aporta un dato realmente esencial para la visualización, los habitantes por zona de transporte local.
En la presentación de GH calculábamos las áreas de transporte local y vecindades por su relación geométrica, a través de cuadrículas delimitadas por las distancias entre vías. En este caso y para un trabajo más interesante hacia el estudio de la densidad, las compondremos a partir de un número máximo de habitantes por zona, utilizando la división matemática del árbol cuaternario que nos permite condicionar rectángulos a partir del número de puntos en su interior. Esta operación le añade el protagonismo que merecía al estudio sobre la población y nos aporta un dato realmente esencial para la visualización, los habitantes por zona de transporte local.
– Vías principales: 300-500 hab.
– Vías secundarias: 20-40 hab.
– Celdas mínimas: 10 – 30 m.
El conjunto de puntos exteriores aparecen como generadores de una primera distribución (por proximidad) que nos elimina aquellas casillas con un valor = 0, encontrando con esto nuestro primer perímetro de trabajo por distribución de población en un diálogo entre contextos de atracción los filtros sobre el estudio geométrico que ya teníamos. Podemos comprobar las áreas de influencia en función de las cargas atractoras por cada punto.
FASE 1. DISTRIBUCIÓN
FASE 2. CÁLCULO
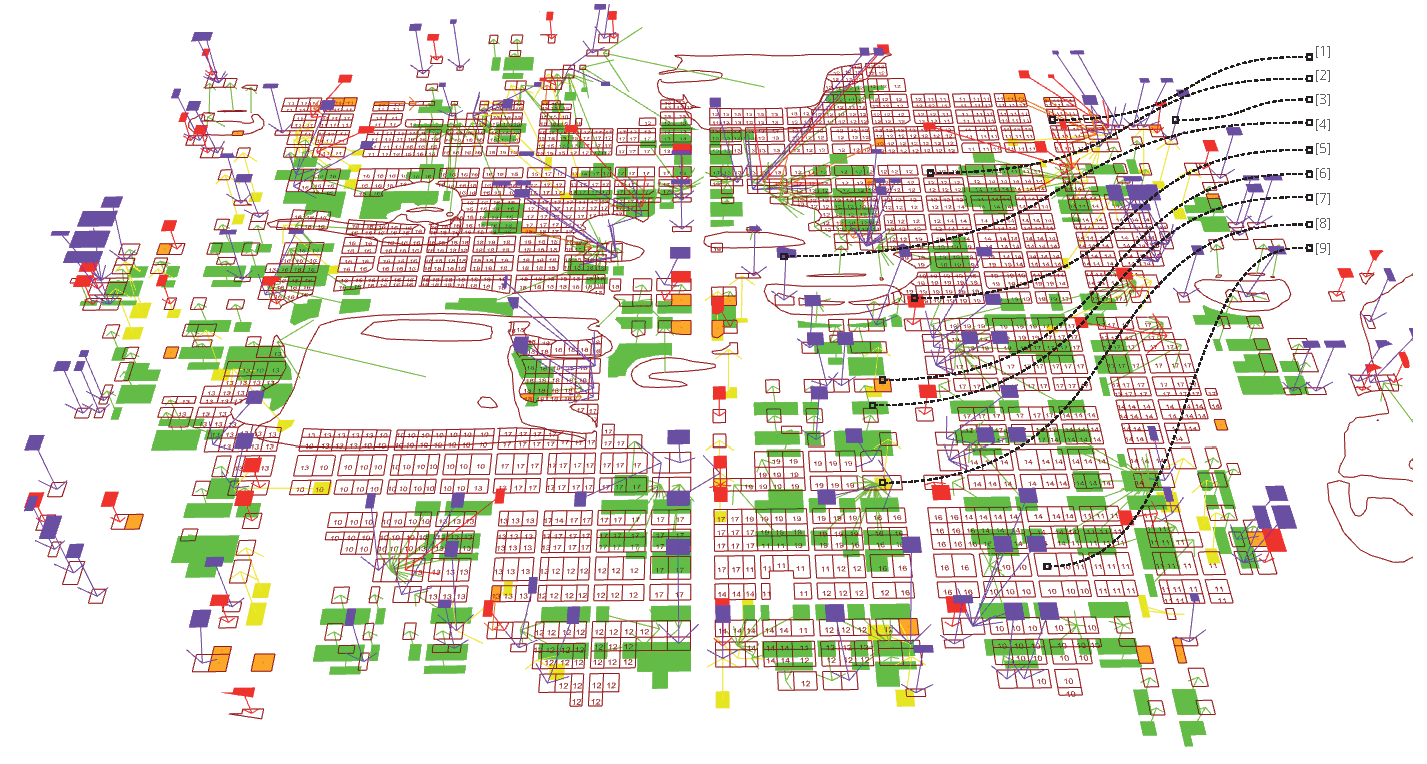
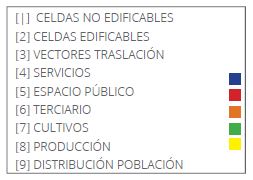
Para llegar hacia un mapa común a partir de las distribuciones por usos, necesitamos decidir sobre la escala con la que trabajamos. En este caso empleamos la división por celdas mínimas como espacio de medida receptor de los datos distribuidos. El sumatorio de cada una de las listas por celda se convierte en el primer dato para diferenciar entre celdas “edificables” y “no edificables”, pero también podremos condicionar otros límites.
En este caso concreto, y tomando los generadores de diversidad para la vitalidad urbana de Jacobs donde el distrito ha de cumplir más de una función primaria, preferiblemente más de dos, condicionamos la edificabilidad de estas celdas obligando a que nunca haya más de un uso ausente para el cálculo siguiente.
FASE 3. RECEPCIÓN DE DATOS
CONCLUSIÓN
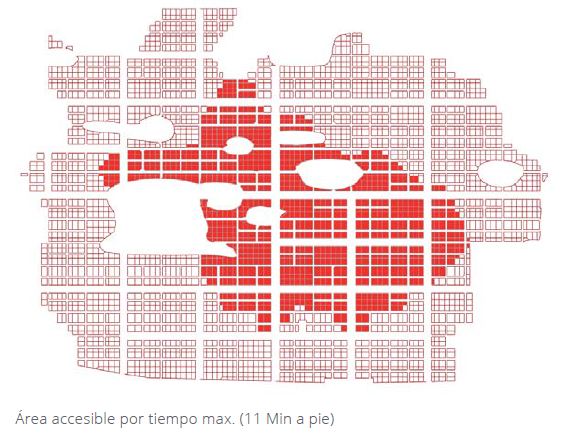 Esta combinatoria que obtenemos en el experimento es lo suficientemente potente como para considerar válidos los conjuntos de la “recepción de datos”.
Esta combinatoria que obtenemos en el experimento es lo suficientemente potente como para considerar válidos los conjuntos de la “recepción de datos”.
Es cierto que al tratarse de un caso que ha sido configurado a través de un cálculo estático, no nos ha permitido introducir periodos temporales para la retroalimentación entre los enlaces de cada uso y la edificación. Esto de por sí, ya supone un enfoque lo suficientemente complejo y por ello hemos preferido aislarlo y trabajarlo en el último experimento.
Precisamente por esta limitación también podemos poner en crisis la localización última del mapa de celdas por usos. Es decir, al estar condicionada dicha secuencia en un momento después de la búsqueda de una edificación optima, la distribución por usos que se compuso en el mapa comun para esta edificación, debe recolocarse sobre los espacios restantes, sin que esto refleje una patología para los habitante en el siguiente turno, pues no lo hay.
 Esto que es un defecto para nuestra analogía nos aporta, por otro lado, un dato de control muy cercano a la simulación urbana. Lo hemos hecho llamar “el valor de suelo” y marca el límite, mediante la combinatoria de dos valores distintos, para conocer si una celda se considera habitable o no. Estos valores se podrían interpretar como la consecuencia del precio del terreno urbanizable y de la exigencia del usuario para encontrar su lugar adecuado en la ciudad, segun el acceso a los servicios y transporte a los que dispone.
Esto que es un defecto para nuestra analogía nos aporta, por otro lado, un dato de control muy cercano a la simulación urbana. Lo hemos hecho llamar “el valor de suelo” y marca el límite, mediante la combinatoria de dos valores distintos, para conocer si una celda se considera habitable o no. Estos valores se podrían interpretar como la consecuencia del precio del terreno urbanizable y de la exigencia del usuario para encontrar su lugar adecuado en la ciudad, segun el acceso a los servicios y transporte a los que dispone.
Aunque entendemos sus defectos de desarrollo, consideramos este experimento como un paso cualitativo en el control de la herramienta y una base realmente potente para la complejización final. Para la siguiente experiencia cabe preguntarse:
¿Podrían verse afectadas la localización dinámica de las viviendas por las relaciones de competitividad entre los vecinos de las barriadas?
¿Podríamos incorporar en el estudio temporal, un sistema de entramado donde cada uso reaccione al resto, incluyendo el residencial, a partir de una matriz de coeficientes?
Acabamos estos potenciales con las palabras de Darke que nos llevan a poner atención sobre estos procesos:
El diseñador comenzaba por enumerar exhaustivamente los factores pertinentes, y luego consideraba las interacciones entre estos factores, estableciendo límites de rendimiento en aquellos factores que podrían tratarse de este modo. Sólo entonces se iniciaba la síntesis de los requisitos para generar una forma, a partir de grupos de factores relacionados. Era de esperar que la síntesis de diversos factores generaría casi automáticamente una “forma”, con la mínima necesidad de que el diseñador ejerza juicios subjetivos; la subjetividad está llena de riesgos, una amenaza para una buena solución.
DARKE, J., The Primary Generator and the Design Process. Design Studies 1 (1) pp. 36-44. (1979)