El medio más fácil de captar mentalmente los problemas es imaginando, en primer lugar, que el suelo del conjunto – salvo el destinado a las calzadas de las calles – es un lugar limpio y vacío; encima de él flotan las casas de apartamentos […] En esta casi pizarra limpia pueden hacerse todo tipo de cosas.
JANE JACOBS
The Death and Life of Great American Cities (1961)
Para poder entrar en estas practicas sobre la Nueva Ciencia de las Ciudades nos serviremos de las palabras de Jacobs buscando en el vacío inicial el potencial de los modelos virtuales. Como veíamos en la presentación, tanto Grasshopper como Netlogo (a partir de ahora también nombrados por sus acrónimos GH y NL, respectivamente) nos ofrecen el caldo de cultivo suficiente para combatir el posible escepticismo de incluir este tipo de herramientas en nuestros opacos procesos de diseño.
Aunque los propositos de este experimento, convertido por lógica en dos subproyectos, es por su identidad presentar las herramientas, entraremos a especificar propositos particulares, consecuentes de infraestructura propia de cada plataforma.
EXPERIMENTO A_1: PRESENTACIÓN GRASSHOPPER
¿Cuál es el propósito del modelo?
Estudiar el reparto distribuido de habitantes en un entorno urbano genérico a través de una serie de patrones geométricos y los atractores propios de las zonas de cultivo, en una situación estática.
¿Cómo utilizaremos la herramientas y su interfaz?
Como herramienta de diseño espacial generativa que es, GH nos permite el control geométrico sobre un entorno tridimensional, añadiendo a las representaciones el potencial para importar datos condicionantes o del entorno.
Centraremos pues nuestros esfuerzos en esta plataforma en la incorporación de aquellos patrones sobre control espacial que detallamos en la sección PdC. Este experimento de presentación solo alojará el cálculo de cultivos que consideramos suficiente como ejemplo explicativo. Será en el experimento siguiente donde se crucen los datos de todos aquellos patrones de manera combinada.
Dividiremos el experimento en fases:
FASE 0: Entrada
FASE 1: Zonificación
FASE 2: Población y atractores
FASE 3: Recepción de datos
Reflexionaremos sobre cada decisión espacial y gestión de datos.
FASE 0. ENTRADA
Se presentan una serie de valores de entrada distintos que van desde los puramente geométricos a los compuestos como condicionantes estadísticos. Esta suma nos permite un traslado suficiente algunos de los contextos de implantación más importantes.
Con la posibilidad de gestionar la topografía como malla, podemos conocer las pendientes de cada cara de ésta y filtrar los datos hacia una zona “urbanizable”, por su restricción constructiva. Su gradiente en % se calculará respecto al plano X.
El ángulo de soleamiento nos segrega valores de “habitabilidad” en este caso según su orientación. Los radianes de esta exposición se suponen cuestionables según el valor de latitud/longitud y las necesidades del proyecto.
Disponemos una serie de puntos exteriores, argumentados sobre el contexto, que aparecerán más tarde como generadores del primer perímetro de estudio
FASE 1. ZONIFICACIÓN
El control geométrico nos permite trazar tres sectores de movilidad distintos en función de las necesidades y escalas de transporte estudiadas en PdC. Utilizaremos para la división distancias mínimas/máximas respecto a la malla genérica. Más adelante gestionaremos estos sectores de transporte local y vecinal únicamente por sus repartos de población.
– Vías principales: 0.5 – 3 km.
– Vías secundarias: 0.1 – 1 km.
– Celdas mínimas: 10 – 30 m.
FASE 2. POBLACIÓN Y ATRACTORES
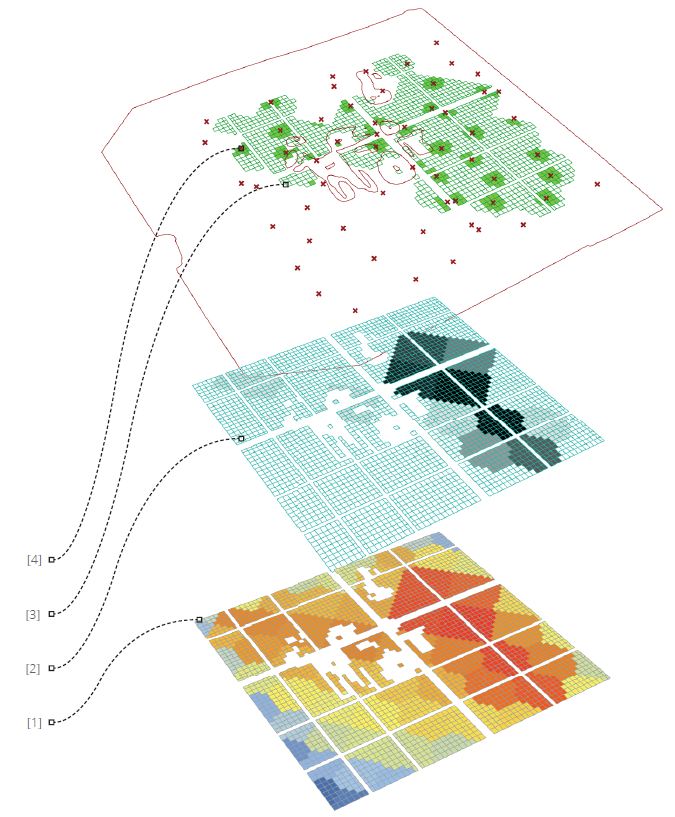Dentro de la herramienta, y gracias a los add-ons de gestión geométrica de Morphocode, podemos encontrar el tipo de aplicación con una cercanía a los estudios de distribución de población que necesitamos para avanzar en la lógica urbana. Considerando cada habitante como un punto en el espacio, contrastaremos los datos sobre sus coordenadas de posición con las del estudio de celdas mínimas del terreno.
A partir de esta relación se pueden dar lugar distintas distribuciones, policéntricas o no, de los correspondientes puntos/habitantes:
– Distancia a la red: Encuentra la distancia de cada segmento de la red (punto medio) hacia un punto o grupo de puntos de atracción.
– Proximidad: Según estos puntos de atracción indicamos que zonas se encuentran más cercanas de todos ellos. Cruza los datos de esas distancias totales para indicar cuanto de cerca está cada celda de todos los puntos a la vez.
– Vecindad: Según estos puntos de atracción indicamos que zonas se encuentran más cercanas de cualquiera de ellos. Encuentra la distancia total a cualquier punto de atracción e intuitivamente nos dice cuanto de cerca está un lugar de cualquiera de esos puntos.
– Zonificación(Voronoi): Encuentra zonas alrededor de puntos de atracción cuyos lugares estén más cercanas a los correspondientes puntos de atracción que a cualquier otro.
Podemos comprobar las atribuciones e interpretaciones tan distintas que generan estos repartos, teniendo en cuenta además que su combinatoria permitiría estudios complejos de “optimización” como aquellos vistos con B. Hillier o M. Batty.
FASE 3. RECEPCIÓN DE DATOS
La recepción de datos que nos aporta este primer ejemplo es realmente limitada, pero al tener un objetivo de muestreo simple y presentación, no se hacía tan necesaria.
Los conceptos más importantes que aparecen en estas imágenes y que nos servirán para los siguientes experimentos son el estudio de transporte por su geometría, las distintas distribuciones de población y, como consecuencia directa, la extrusión de una alegoría a la edificación sobre la malla del terreno inicial.
Por último, y a partir del cálculo del camino más corto, partiendo del algoritmo de ruta más corta de Dijkstra, podremos visualizar la optimización del recorrido entre dos puntos cualesquiera, teniendo en cuenta el estudio de la topografía o no.
EXPERIMENTO A_2: PRESENTACIÓN CON NETLOGO
¿Cuál es el propósito del modelo?
Estudiar el comportamiento, debido a sus afinidades, de tipos distintos de habitante a lo largo del tiempo en un entorno urbano genérico. Utilizaremos un reparto inicial de usos y reglas dinámicas para la aparición de zonas residenciales y la multiplicación de las familias en juego.
¿Cómo utilizaremos la herramienta y su interfaz?
Como herramienta multiagente que es, NL nos permite la gestión individual por agentes a partir de la incorporación de sus afinidades con el entorno, añadiendo a su visualización un potencial en el estudio de movimiento autómata.
Una vez instaladas las reglas de juego sobre el entorno (patches) y sobre los pobladores (turtles), la capacidad de movimiento de éstas últimas les permitirárá desplazarse por el mundo buscando la “felicidad”. Con ésto conseguiremos una estadística evolutiva para determinadas situaciones.
Compondremos el estudio por fases vitales, análogas al campo de estudio, que permitan mediante unas reglas de descendencia comprobar la deriva de determinados tipos de familia, lo que nos explicará, por su declive, las capacidades de supervivencia no solo de los habitantes con afinidades distintas, sino del propio contexto como espacio habitable.
Centraremos pues nuestros esfuerzos en esta plataforma en la incorporación de aquellos parámetros sociales que detallamos en la sección SOC.
ENTIDADES Y PLANTEAMIENTO
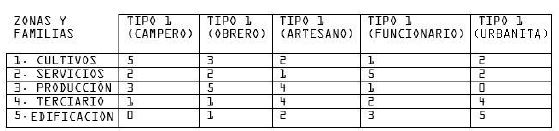5 tipos de patches, 4 iniciales:
– Cultivos [ 
]
– Servicios [ 
]
– Producción [ 
]
– Terciario [ 
]
Y una quinta consecuente de la “felicidad” de los individuos.
– Edificación [ 
]
Definimos 5 agentes [ 
] correspondientes a tipos de familia distintas con 5 valores de afinidad respecto a cada uno de los patches (Del 1 al 5).
– Campero
– Obrero
– Artesano
– Funcionario
– Urbanita
Entraremos a definir también una unidad esencial de tiempo: cada tick del programa corresponderá a un año para las familias. Podremos configurar el número de ticks por fase pero tendremos que tener en cuenta que cada familia como máximo puede vivir 2 fases y tener descendencia solo al final de la primera.
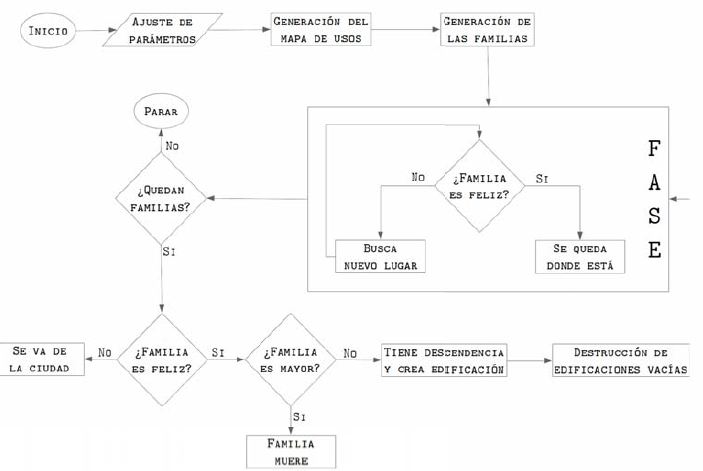
Funcionalmente el modelo intercambia información principalmente por el comportamiento de las familias (turtles) que recorren el mundo (patch) buscando un lugar adecuado para establecerse y tener descendencia. Esta “felicidad” abstracta, además de por las afinidades dependiendo de su tipo, quedará definida por unas propiedades globales que afectarán a todas las familias:
– Visión-personas: capacidad de movimiento por turno.
– Radio exterior: define el área de recepción de patches.
– Umbral: Sumatorio de pesos de los patches dentro del radio exterior.
Junto al reparto de usos y las propias familias, configuramos estos valores como editables por el observador, pudiéndo darse múltiples situaciones bajo su control.
En la imagen podemos comprobar el diagrama secuencial que ocurre dentro del código, donde aparecen intrínsecas las reglas de supervivencia del sistema.
Estas situaciones que aqui aparecen, se dieron lugar dentro del encuentro donde se desarrolló este experimento-presentación de NL, las jornadas FORMA 14, organizadas por la ETSII de Sevilla. (Oct. 2014)
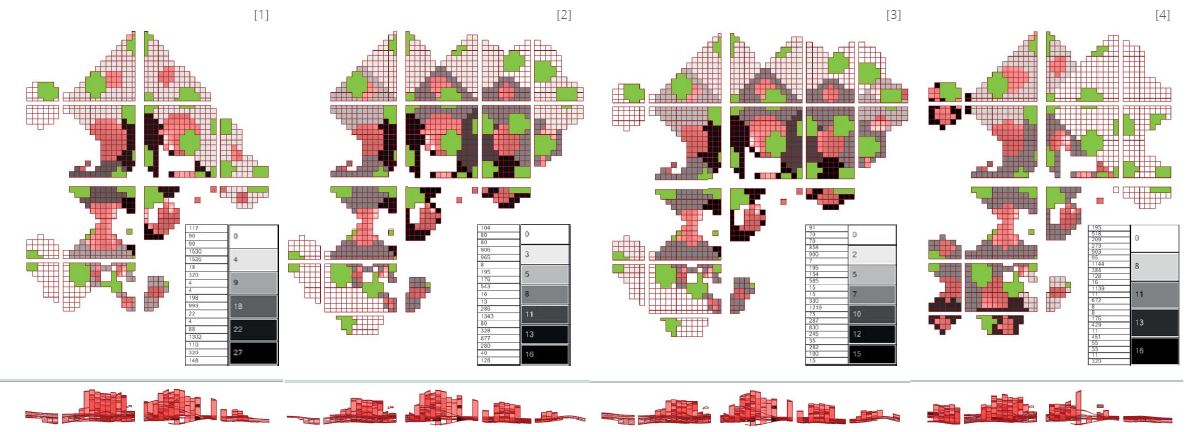
Las situaciones de los patches que vemos en las imagenes nos muestran la diferencia de esos momentos intermedios que pueden generar a partir de un código relativamente sencillo. Planteados los datos de entrada a partir de unas intuiciones iniciales, la recepción de los datos de cada secuencia nos provocó un aprendizaje inesperado.
CASOS DE ESTUDIO
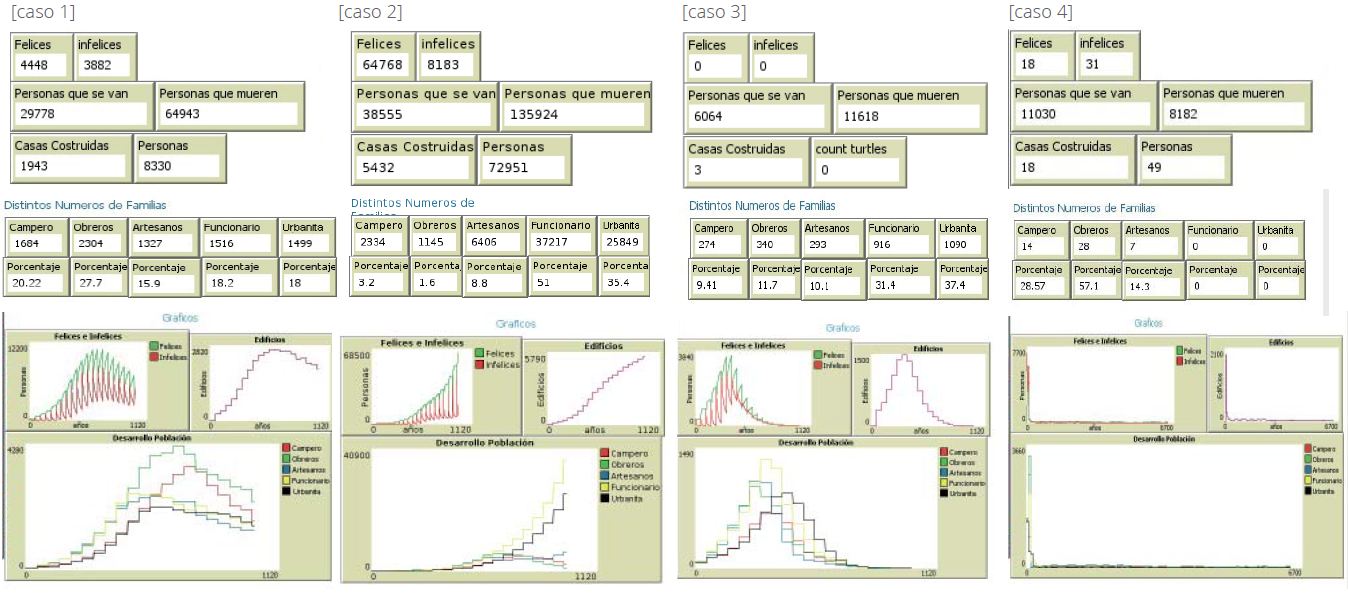
CASO 1
– Inicio estandar (25%)
– Predicción curva población suave
CASO 2
– Inicio abundancia de cultivo.
– Proceso desarrollo muy rapido.
– Predicción de una gran ciudad y aumento de la población de familias urbanas, generando el consecuente declive.
CASO 3
– Corta vision familias
– Predicción pequeños nucleos de población (muy densos)
– Sustitucion aleatoria de usos generará un mapa final sin datos relevantes.
CASO 4
– Traslado poblacion EXP A_1.
– Gran competencia inicial.
– Predicción confusa.
– Sustitucion coherente generará un mapa final muy útil.
RECEPCIÓN DE DATOS
Los datos que podemos recibir en este tipo de plataforma son tantos como los que configuremos en su código. En nuestro caso hemos decidido recibir los siguientes valores absolutos :
– Número de familias felices/infelices
– Suma de familias que se han ido del patch.
– Suma de familias que “mueren”.
– Casas construidas y familias presentes en ese momento.
Y configurar en base a éstos un conjunto de gráficas en el tiempo:
– Número de edificios
– Número de familias felices/infelices
– Número de personas de cada familia.
La plataforma NL permite una configuración de los valores editables al inicio del experimento, pero también la modificación en cualquier momento por el observador, que en este caso seríamos el equipo de diseño.
En los cuatro casos de estudio podemos extraer analogías muy interesantes respecto al comportamiento de la población. Dentro del anecdotario lúdico, me gustaría resaltar el caso tan especial del cuarto ejemplo, donde por una gran competición inicial, causada por la introduccion de un número simbólico (7000) pero excesivo de familias, se redujo la población a pequeños grupos de 10-20 familias a los pocos años del experimento. Éstos asentamientos compuestos por las 3 clases sociales más “bajas”, o “sensibles” con los recursos, según queramos entenderlo (Campero, Obrero y Artesano), llegaron a un estado de armonía con una duración casi 10 veces más años (ticks) que el resto de casos.
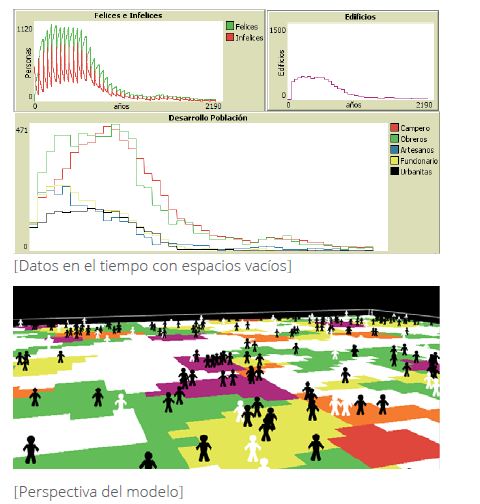
La relación de la edificación al retirarse del tablero de usos nos aporta datos muy distintos dependiendo de como la configuremos.
Si el uso que la sustituye es aleatorio, no nos resultarán utiles las imagenes finales en la fase de conclusión.
Si el uso que la sustituye es relativo a los que le rodean cuando se destruye, nos puede generar un mapa visual realmente rico, indicando a través de la agrupación de usos del mundo (patches) la tendencia de ese proceso evolutivo, tambien hacia la gestión del suelo.
CONCLUSIONES
El caso del primer submodelo, como vemos en sus resultados, fue parte de un proceso de formación personal en el lenguaje de GH; el segundo, tal como ya se explicó ántes, respondía al caso de estudio de unas jornadas sobre programacion en NL, por lo que se apartaron las pretensiones de una parametrización social válida, sustituyendola por un proceso enfocado al conocimiento de los modelos multiagente.
Aun así las conclusiones sobre los propositos iniciales, y aún tratándose de experimentos iniciáticos, son múltiples. Para explicar las decisiones en esta dinámica experimental volvemos a hacer una diferenciación por lenguajes:
CONCLUSIÓN GH
Después del análisis del reparto, tomaremos la distribución policéntrica por proximidad como la relación primaria para la cuestion de población de los siguientes experimentos.
Comprobada la insuficiencia de un estudio de un solo uso, utilizaremos la conjunción de suelos suficiente para considerar habitable cada una de las celdas de estudio.
Conociendo el potencial de representación, emplearemos las extrusiones de las celdas para mostrar distintos datos complementarios, desde las distancias a las combinaciones de usos a la edificabilidad por planta.
CONCLUSIÓN NL
Necesitaremos desarrollar la siguiente aplicación con una visión más complejizada hacia los tipos de familia, el terreno y su capacidad pues de importación de valores de futuros contextos.
Trabajaremos el concepto del espacio vacío generando una reflexión alrededor del uso del suelo yermo, aquel que no alimenta las afinidades de sus habitantes. Un valor importante para poder integrar situaciones de ciudades ya consolidadas.