Utilizando el título del libro de Michael Batty, The New Science of Cities27, buscamos el enlace adecuado entre las dos partes diferenciadas de nuestro Estado de la Cuestión. Batty28 se ha convertido en la referencia de aquellos argumentos de investigación compleja sobre las ciudades y también en nuestro punto de inflexión. El autor introduce una serie de herramientas para la simulación urbana que abarcan desde simples modelos estocásticos29 evolutivos a estudios complejos de zonificación. El análisis implícito sobre las decisiones y predicciones, a través de sus interacciones y flujos, es tremendamente importante para el estudio de las ciudades futuras.
Igual que pasaba con Hillier30, Batty se sumerge en las posibilidades de las ciencias de computación dentro del marco urbano, aunque es cierto que desde una perspectiva más actualizada – debido a la fecha de publicación de ambas investigaciones – y aún más específica. – gracias al desglose de sistemas de cálculo en una matemática compleja.
Los nuevos métodos de probabilidad y estadística dieron más exactitud y alcance, hicieron posible una visión y un tratamiento más olímpico de los supuestos problemas de la ciudad.
JANE JACOBS. Muerte y vida de las grandes ciudades, (Capitan Swing, 2011) originalmente publicada como The Death and Life of Great American Cities (1961)
SISTEMAS COMPLEJOS
Desde aquellos métodos de probabilidad que le preocupaban a Jacobs, podemos profundizar en los argumentos hacia la parametrización presentes en el trabajo de Batty.
Equilibrio y dinámica:
Un estudio aceptable de las ciudades debe adoptar una dinámica que permita directamente simulacros en escenarios de crecimiento diferentes, aflorando criterios de equilibrio y estabilidad. Los modelos de simulación urbana fueron los primeros en hacer frente a esta dinámica. Tuvieron unos avances lentos pues en su momento, una teoría más amplia, de cómo el cambio se lleva a cabo en las ciudades, se estaba desarrollando.
Patrones y procesos:
La idea de utilizar la morfología como un detonante para detectar los diferentes patrones subyacentes en el proceso de las ciudades, se relaciona con el trabajo de Kevin Lynch31, y consecuentemente con autores que ya hemos visto como Jacobs o Alexander.
Interacciones, flujos y redes:
Estas definiciones componen las entidades que tienen lugar en las ciudades y que atraen a los habitantes para producir e intercambiar ideas. Los puertos y nodos de atracción generan aglomeraciones y estas a su vez al crecer y formar parte de una red, infl uyen en nuevas conexiones. Podemos encontrar en esta diferenciación infl uencias claras del trabajo de Grahame Shane32 sobre las heterotopías de Foucalt.
Evolución y aparición:
Los patrones emergen de los procesos y propagan sus efectos a través de diversas formas de segregación y difusión. Si definimos el paisaje urbano como una rejilla y un barrio como las ocho celdas alrededor de cualquier celda dada, en la cual se instalará la semilla, podríamos llevar a cabo un desarrollo alrededor de esta unidad a través de un cierto patrón local de invariabilidad. Este estudio sobre patrones fractales y autómatas celulares recuerda profundamente a las investigaciones de John Conway33 y su Juego de la Vida.
Tamaño, forma y escala:
Las ciudades cambian claramente su forma como cambian su tamaño, y por lo general lo hacen en una alometría34. Hay muchas consecuencias relacionadas con el tamaño de la ciudad: El coste efectivo, las zonas verdes, la densidad, pero una de las más importantes es la frecuencia de los objetos a esas diferentes escalas. Dicha distribución es determinada por la competición por los limitados recursos, llamada la regla rango-tamaño (una aplicación de la Ley del mínimo esfuerzo35), y se aplica, por supuesto, no solo en los tamaños de las ciudades y sus fenómenos relacionados, sino en la evolución del tamaño de los nodos en las redes libres de escala36. El Modelo Barabási–Albert37 aparece en los cálculos de Batty y también en los nuestros.
CONSTRUYENDO UNA CIENCIA DE LAS CIUDADES
Gracias a Batty, y en clara referencia a Stephen Wolfram38, nos sentimos forzados a llevar nuestro entendimiento sobre el diseño de las ciudades a términos de ciencia, y esto nos obliga a revisar nuestras axiomas en particular, ya que muchos se acercan al estudio de la ciudad como una forma de arte, mientras que otros lo consideran en un contexto humanista más amplio.
Por ciencia nos referiremos a un cuerpo de conocimiento organizado que usa herramientas comunes y métodos que pueden ser reproducidos una y otra vez por diferentes individuos. El conocimiento producto de esto puede llegar a ser muy diferente según el caso, llegando a variaciones importantes aunque con un criterio clave, explícito y transparente. Como veíamos en nuestra presentación, la transparencia respecto a los nuevos programas de diseño, cercanos a estas definiciones de ciencia que aquí exponemos, influenciaron desde los textos de Herbert Simon39 a múltiples autores, y Batty es uno de ellos.
Si hay que tener algo en cuenta es que no hay una sola aproximación que pueda ser aplicada en todos los sitios y por todo el mundo, pero sí hay invariantes y regularidades que pueden ser aprovechadas en nuestra preocupación por un diseño de mejores ciudades. Por tanto entiéndase el análisis de Batty, y nuestra reflexión, tal como él lo explicitaba: el desarrollo de “una” ciencia de las ciudades, no necesariamente “la” ciencia.
A partir de estas explicaciones debemos comenzar a exponer la serie de términos utilizados en esta ciencia de las ciudades. Un lenguaje dentro de las herramientas usadas, y cuya concreción nos servirá de enlace para llegar a las entidades urbanas.
Puntos
Son la realidad más simplificada. La representación de los objetos cómo localizaciones, como lugar inicial en los problemas a tratar. Con un número de objetos (j), elementos asociados a unos atributos (k) definidos en la matriz NxM {Aik}, podemos llegar a comparar dichos elementos en función de los atributos que tienen en común o los propios objetos en común.
Flujos
Aparecen dentro del método usual de visualización que explora los enlaces entre entidades geométricas distintas. C on un número de objetos (i), elementos asociados a unos atributos (k) definidos en la matriz NxM {Aik} podemos llegar a comparar dichos elementos en función de los atributos que tienen en común o los propios objetos en común. Un flujo puede ser una proyección de los vectores direccionales desde los orígenes a sus destinos o unas líneas de deseo en el modelado del transporte. Como a mayor número de orígenes y destinos el número de líneas que se cruzan se incrementa hasta aproximadamente el cuadrado del número de localizaciones (N2), nuestra capacidad para discriminar patrones de tales mapas de flujo se volverá cada vez más difícil. Esto tiene mucho que ver con aquel modelo de Barabási.
Grafos
Nodos, hubs y vértices son usados para definir los elementos o componentes básicos de los grafos, y links, arcos o ejes usados para especificar las relaciones entre los elementos. Las comparaciones podremos mostrarlas como gradientes o de forma binaria. Comparando la matriz de distribución (F), podremos encontrar patrones y procesos asociados a dichas conexiones. Comparar la matriz alternativa (H) y sus operaciones, nos dará un vasto rango de posibles estructuras de flujos y análisis de redes. Un considerable foco en la ciencia de redes no es tanto la estructura de grafo, al menos directamente, sino sus propiedades estadísticas, en las cuales se enfatiza la distribución de los enlaces que originan o están destinados para diferentes nodos.
Unos gradientes suficientes en las relaciones de los grafos multicapa nos llevarán a experimentos realmente potentes que trabajen con la matriz de coeficientes propia de un sistema complejo.
Añadir una variedad de puntos de trabajo complejiza enormemente la representación de estos flujos, y por supuesto los grafos posibles. Históricamente, esta puede ser la razón por la cual estos tipos de mapas múltiples casi no aparecieron hasta los inicios de las computadoras.
CIENCIA DE LAS CIUDADES
Como en Space Syntax no solo se analizaran aquellas redes del espacio euclidiano sino los conjuntos de relaciones que tienen diferentes grados de compromiso con el espacio. Desde redes cuyos nudos si se componen en localizaciones especificas pero sus enlaces no lo hacen, a redes sociales donde tanto los nodos como sus enlaces deben estar continuamente en movimiento y no se asocian de ninguna manera con lugares específicos del espacio. Sí es cierto que todas estas redes que se examinan tienen alguna asociación espacial, en el sentido que siempre pertenecen a las ciudades o su planeamiento físico.
Si a este gran aprendizaje sobre el trabajo de Michael Batty, incluimos las capacidades de representación tridimensional, podremos llevar el espacio de trabajo de nuestras aproximaciones prácticas a la complejidad de un marco urbanístico.
Para entender este traslado a valores enteramente urbanos y conceptos alrededor del ámbito de la predicción, usaremos el “juguete”, así lo definía el mismo, que Batty emplea para explicar la generación de soluciones a un problema de ciudad.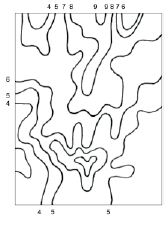
En este ejemplo de referencia, Batty calcula el desarrollo residencial de un pequeño pueblo inglés. Con una población de 50000 habitantes, identifica 12 (K) objetivos clave que se formulan como factores críticos al problema. Este conjunto de factores está casi con certeza incompleto y por lo tanto el problema es algo hipotético. Sin embargo, sirve como un buen ejemplo con el que demostrar la capacidad de parametrización de dichos factores y su confluencia.
Los valores representados son:
Ai1: Accesibilidad a servicios urbanos existentes.
Ai2: Costes del suelo.
Ai3: Accesibilidad a los servicios recreativos.
Ai4: Áreas de microclima aceptable.
Ai5: Áreas de captación de agua y de drenaje defi ciente.
Ai6: Limitaciones institucionales del gobierno.
Ai7: Accesibilidad a los mercados urbanos externos.
Ai8: Excesiva contaminación industrial.
Ai9: Áreas de topografía adecuada.
Ai10: Zonas de esparcimiento rural.
Ai11: Áreas históricas urbanas.
Ai12: Zonas de alta calidad agrícola.
El proceso de distribución se realiza en este caso de manera binaria, donde el color negro implica que la localización en cuestión no puede ser desarrollada mientras que el color blancomuestra lo contrario. Cada uso de la tierra se convierte en una comparación con la solución final, superando la superposición clásica. La diferencia esencial entre estos métodos y los que existían anteriormente, gira en torno a la evaluación relativa de los muchos factores en conflicto, llegando a un conocimiento exhaustivo de aquellos que determinan el éxito o no de algunas soluciones para el problema de la localización óptima convergente. En esencia, el orden en que estos factores podrían ser comparados entre sí, refleja la importancia relativa de cada uno dentro de la “mejor” solución. Tradicionalmente, los planificadores han presentado tales factores en términos de su conveniencia o idoneidad (o no) para resolver el problema dispuesto.
Esto es importante y nos dice que los sistemas son elegidos deliberadamente por el diseñador, por lo que podría formar parte de una mala decisión. Pero esto no es tan importante como comprobar en qué fase de la producción de ideas empezamos nuestro proceso de diseño y sobre todo, tal como comentábamos, la transparencia de sus errores. Probablemente el mejor de estos métodos fue el expuesto por el ya citado Christopher Alexander40 en 1964, que argumentó que cada factor relevante para el desarrollo, por lo general, supone al menos una solución óptima al problema. Entonces el trabajo del diseñador se convierte en examinar cada una de estas sub-soluciones y tratar de conciliarlas en cuestiones de ubicación con el resto.
El proceso de generación del diseño, por tanto, implica algún tipo de promedio. Exploraremos, gracias a la labor de Batty, un método iterativo que sintetice las sub-soluciones de un modo que obtengamos un resultado con un compromiso verdadero o, en sus palabras, un mejor promedio.
Hay varias maneras en las que explorar estas estrategias para la ponderación. Además de un método comparativo por parejas, el método conocido como proceso analítico jerárquico desarrollado por Saaty41, ha sido profundamente aplicado en prácticas para la derivación de conjuntos de fuerzas. Este tipo de análisis ya fueron competentemente usados en diferentes prácticas de planeamiento sobre zonificación42. Encontramos un enorme potencial del cruce de estos métodos con los sistemas de información geográfica (SIG).
El siguiente paso del trabajo recaía indudable sobre las secuencias, incluyendo bucles de información y su relación en el tiempo. Asumiendo que cada diseñador/agente es capaz de llegar a un perfecto compromiso entre su visión y las del resto, el proceso de resolución de confl ictos establece una relación íntima con las ecuaciones de Markov43:
– En un primer ciclo t, cada diseñador/agente transmite una visión a través de los canales al resto de diseñadores.
– Cada agente cambia su visión tomando las consideraciones que surgen entre su propia visión y las del resto.
– Entonces en el siguiente ciclo t + 1 estas nuevas visiones surgen de nuevo de la misma manera. Solo se llegará a un consenso a través de estructuras fuertemente conectadas pues serán las que permitan la visión en los dos sentidos por parte de los agentes.
– La continua transmisión de visiones comprometidas acaba gradualmente reduciendo las diferencias entre agentes, mostrando el potencial o declive del grupo.
Todo esto sucede en sistemas fuertemente conectados y como cada factor se encuentra interconectado, es evidente que el conjunto inicial, cuanto más avance el sistema, tendrá menos influencia sobre la solución final. Cumple la ausencia de memoria en la transición de estados.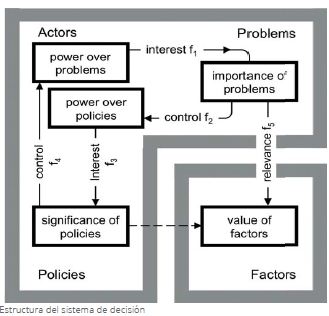
Como se puede empezar a deducir, la selección de la máquina “óptima” es quizás el concepto más especulativo de esta teoría referente al propio diseño de las máquinas de diseño. Es fácil ver las diferencias entre las diferentes máquinas empleadas y ver que algunas se adaptan mejor que otras, pero es muy difícil revisar con criterios relevantes cuál debiera ser nuestra elección. Tal como explica Batty, esta ciencia es sugestiva, no definitiva, para problemas de las ciudades o del planeamiento de las ciudades que requieran de aproximaciones múltiples que envuelvan además, a múltiples partes interesadas. El propósito de la ciencia es informar del diálogo complejo, no generar respuestas o soluciones, al menos no de la manera que se entendían.
ACCIÓN COLECTIVA
El uso del término diseñador/agente que se hizo en la secuencia, fue claramente intencionado, pues estos procesos se pueden llevar tanto a las entidades competitivas en un modelo virtual como a las jerarquías de poder que se producen en las fases de diseño urbano.
Es en este contexto liberado donde la ciudad surge como un artefacto, como un producto más allá del proceso. La forma toma el lugar de la función comenzando a dominar nuestros modelos y el cómo los elementos de la ciudad se relacionan los unos con los otros y la provienen de dinámicas de cambio.
Hay muchas maneras de elaborar este paradigma. Por ejemplo una de ellas es que el planeamiento debe ser la base para un sistema de transacciones y comunicaciones de pequeños grupos, una parte integral de la teoría de las relaciones sociales. Esto significaría que la manera de llegar a mejores decisiones no viene por un sistema de optimización, tal como este se puede entender; sino por un proceso de negociación y compromiso entre las partes.
Estos modelos como veremos en adelante se utilizaron también para estudios sobre el poder social.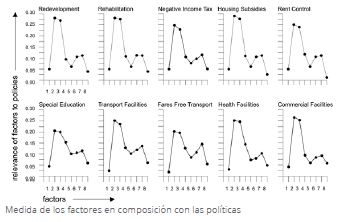
Nuestro estudio sobre el autor termina con uno de los últimos trabajos prácticos realizados por el equipo de Batty. Esta aplicación que se encuentra explicada también en The New Science of the Cities, explora la relación de poder y afi nidad de un grupo de actores trabajando sobre el problema de la “pobreza” dentro de la ciudad.
Los actores(A), problemas(Pr), políticas(P) y factores(F) que participan en este caso de estudio son:
Como ocurría en la aproximación del desarrollo residencial, y como nos ocurrirá a nosotros, hay muchos elementos importantes excluidos, pero se incluyen los suficientes como para entender las situaciones de los análisis particulares de una manera apropiada.
Los vectores de poder se determinan de manera arbitraria y las ecuaciones son resueltas de forma iterativa. La convergencia hacia un estado de equilibrio por tanto, es rápida.
En este modelo, los controladores de la tierra pública y privada, así como el comité de política presidencial, asumían un considerable poder. A partir de los cálculos se pudieron dar cuenta que ciertos actores tenía más poder de lo que parecía en un primer momento. Podemos comprobarlo tanto en en estas gráficas como en las de la página anterior.
CONCLUSIÓN
Muchos de los aspectos importantes de las ciudades son difíciles de explorar, pero nunca antes esta cantidad de posibilidades configuró un entorno tan rico en el que progresar sobre una nueva ciencia.
Serán otros los que cojan el testigo de los métodos investigados por Michael Batty, demostrando si estas aproximaciones prescriptivas nos llevan a un mejor entendimiento y diseño de nuestras ciudades, que es lo realmente necesario.
BIBLIOGRAFÍA
27 BATTY, M., The New Science of Cities, The MIT Press (2013)
28 Michael Batty, Urbanista y geógrafo brítanico profesor en la UCL y presidente del Centro de Análisis Espaciales Avanzado (CASA)
29 Un proceso estocástico es aquel cuyo comportamiento es no determinista, en la medida que el subsiguiente estado del sistema está determinado tanto por las acciones predecibles del proceso como por elementos aleatorios.
30 HILLIER B. Space is the Machine: A Configurational Theory of Architecture, Cambridge: Cambridge University Press. (1999)
31 LYNCH, K., The Image of the City. Cambridge MA: MIT Press (1960).
32 GRAHAME SHANE D., Urban Design Since 1945: A Global Perspective, Wiley John + Sons Ltd, Londres (2011)
33 GARDNER, M., Mathematical Games – The fantastic combinations of John Conway’s new solitaire game “life”. Scientific American 223. pp. 120–123. (1970).
34 Alometría: Cambios de dimensión relativa de las partes en función a los cambios del tamaño total.
35 ZIPF G. K., Human Behavior and the Principle of Least Effort. Cambridge, Massachusetts: Addison-Wesley. p. 1. (1949).
36 En una red libre de escala, algunos nodos están altamente conectados, es decir, poseen un gran número de enlaces a otros nodos, aunque el grado de conexión de casi todos los nodos es bastante bajo.
37 Algoritmo empleado para generar redes aleatorias complejas libres de escala empleando un mecanismo denominado conexión preferencial.
38 WOLFRAM, S. A New Kind of Science, Wolfram Media, Champaign IL. (2002)
39 SIMON H., The Sciences of the artificial, The MIT Press; 3rd edition (1996)
40 ALEXANDER C, Notes on the Synthesis of Form, (Harvard Paperbacks) Harvard Univ Pr; (1964)
41 SAATY, T.L. The Analytic Hierarchy Process. McGraw-Hill, (1980)
42 WANNOP, R. E. Cálculos para la elección de una estación de repostaje en Plymouth. (1971)
43 MARKOV A.A. La distribución de la ley de los grandes números a valores que dependen unos de otros. Actas de la Sociedad Físico-Matemática de la Universidad de Kazan. (Trad. Ruso).(1906)
*El proceso de Markov estándar computa la probabilidad que tiene el sistema para cada uno de sus diferentes estados, equivalentes a los nodos de la red de diseño o las subsoluciones del problema.